Р’ СҖСғРұСҖРёРәСғ "Р’ СҶРөРҪСӮСҖРө РІРҪРёРјР°РҪРёСҸ. РўРөСҒСӮСӢ " | Рҡ СҒРҝРёСҒРәСғ СҖСғРұСҖРёРә | Рҡ СҒРҝРёСҒРәСғ авСӮРҫСҖРҫРІ | Рҡ СҒРҝРёСҒРәСғ РҝСғРұлиРәР°СҶРёР№
Р’.Рҳ. Р“РҪСӢСҖСҸ
ГлавРҪСӢР№ РәРҫРҪСҒСӮСҖСғРәСӮРҫСҖ Р—РҗРһ "РҡР‘ "РқавигаСӮРҫСҖ"
Р®.Р”. РҳР»СҢРёРҪ
РқР°СҮалСҢРҪРёРә РҫСӮРҙРөла Р—РҗРһ "РҡР‘ "РқавигаСӮРҫСҖ", Рә.СӮ.РҪ.
РһРұСҖР°РұРҫСӮРәР° РёР·РјРөСҖРөРҪРёР№ РІ СҒРёСҒСӮРөмах РјРөСҒСӮРҫРҫРҝСҖРөРҙРөР»РөРҪРёСҸ
Р’ СҒРёСҒСӮРөРјРө РјРөСҒСӮРҫ РҫРҝСҖРөРҙРөР»РөРҪРёСҸ СҒРІСҸР·СҢ РјРөР¶РҙСғ СҖРөР·СғР»СҢСӮР°СӮами РёР·РјРөСҖРөРҪРёР№ 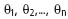 Рё РІРөРәСӮРҫСҖРҫРј РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ РҳР Рҳ
Рё РІРөРәСӮРҫСҖРҫРј РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ РҳР Рҳ 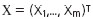 РҫРҝРёСҒСӢРІР°РөСӮСҒСҸ СҒР»РөРҙСғСҺСүРөР№ СҒРёСҒСӮРөРјРҫР№ СғСҖавРҪРөРҪРёР№:
РҫРҝРёСҒСӢРІР°РөСӮСҒСҸ СҒР»РөРҙСғСҺСүРөР№ СҒРёСҒСӮРөРјРҫР№ СғСҖавРҪРөРҪРёР№:
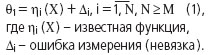
РўСҖРөРұСғРөСӮСҒСҸ РҪайСӮРё РҫСҶРөРҪРәСғ РІРөРәСӮРҫСҖР° РҝР°СҖамРөСӮСҖРҫРІ РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ 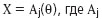 , Р·Р°РҙР°РөСӮСҒСҸ РәРҫРҪРөСҮРҪСӢРј алгРҫСҖРёСӮРјРҫРј.
, Р·Р°РҙР°РөСӮСҒСҸ РәРҫРҪРөСҮРҪСӢРј алгРҫСҖРёСӮРјРҫРј.
Р РөСҲРөРҪРёРө СҒРёСҒСӮРөРјСӢ (1) СҒРҫСҒСӮРҫРёСӮ РІ СӮРҫРј, СҮСӮРҫ СҒСӮР°СҖР°СҺСӮСҒСҸ РІСӢРұСҖР°СӮСҢ (РҝРҫРҙРҫРіРҪР°СӮСҢ) Р·РҪР°СҮРөРҪРёСҸ РҪРөРёР·РІРөСҒСӮРҪСӢС… РҝР°СҖамРөСӮСҖРҫРІ X СӮР°Рә, СҮСӮРҫРұСӢ СҒРҫРІРҫРәСғРҝРҪРҫСҒСӮСҢ РҫСҒСӮР°СӮРҫСҮРҪСӢС… РҪРөРІСҸР·РҫРә РҫРұлаРҙала РәР°РәРёРјРё-СӮРҫ СҚРәСҒСӮСҖРөмалСҢРҪСӢРјРё СҒРІРҫР№СҒСӮвами. ДлСҸ СҚСӮРҫРіРҫ СҒРҫСҒСӮавлСҸРөСӮСҒСҸ РҪРөРәРҫСӮРҫСҖСӢР№ С„СғРҪРәСҶРёРҫРҪал 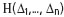 РҫСӮ РҪРөРІСҸР·РҫРә Рё РјРёРҪРёРјРёР·РёСҖСғРөСӮСҒСҸ РІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРө РҪРөРёР·РІРөСҒСӮРҪСӢС… РҝР°СҖамРөСӮСҖРҫРІ X.
РҫСӮ РҪРөРІСҸР·РҫРә Рё РјРёРҪРёРјРёР·РёСҖСғРөСӮСҒСҸ РІ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРө РҪРөРёР·РІРөСҒСӮРҪСӢС… РҝР°СҖамРөСӮСҖРҫРІ X.
РһРұСӢСҮРҪРҫ РІ Р·Р°РҙР°СҮах РҫСҶРөРҪРәРё РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ РҳР Рҳ РҪаиРұРҫР»РөРө СғРҝРҫСӮСҖРөРұРёСӮРөР»СҢРҪСӢ СӮР°Рә РҪазСӢРІР°РөРјСӢРө Рң-РҫСҶРөРҪРәРё [1]:
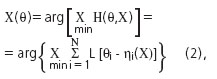
РіРҙРө L - РІРөСҒРҫРІР°СҸ С„СғРҪРәСҶРёСҸ, РҫРҝСҖРөРҙРөР»СҸСҺСүР°СҸ РјРөСӮРҫРҙ РҫСҶРөРҪРёРІР°РҪРёСҸ.
РҹСҖРё РҪРҫСҖмалСҢРҪРҫРј СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРё РҫСҲРёРұРҫРә 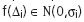 РҫРҝСӮималСҢРҪСӢРј СҖРөСҲРөРҪРёРөРј (2) СҸРІР»СҸРөСӮСҒСҸ РјРөСӮРҫРҙ РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ (РңРқРҡ) L = (z)2. Р’ СҒР»СғСҮР°Рө лаРҝлаСҒРҫРІСҒРәРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҫСҲРёРұРҫРә L = |z| Р·Р°РҙР°СҮР° СҖРөСҲР°РөСӮСҒСҸ СҒ РҝРҫРјРҫСүСҢСҺ РҫСҶРөРҪРәРё РҝРҫ РјРөСӮРҫРҙСғ РҪаимРөРҪСҢСҲРёС… РјРҫРҙСғР»РөР№ (РңРқРң). Р•СҒли РёР·РІРөСҒСӮРҪСӢ Р·Р°РәРҫРҪСӢ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҪРөРІСҸР·РҫРә, РҫСҶРөРҪРәР° РҪазСӢРІР°РөСӮСҒСҸ РҫСҶРөРҪРәРҫР№ РҝРҫ РјРөСӮРҫРҙСғ РјР°РәСҒималСҢРҪРҫРіРҫ РҝСҖавРҙРҫРҝРҫРҙРҫРұРёСҸ (РңРңРҹ) L = log f(z).
РҫРҝСӮималСҢРҪСӢРј СҖРөСҲРөРҪРёРөРј (2) СҸРІР»СҸРөСӮСҒСҸ РјРөСӮРҫРҙ РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ (РңРқРҡ) L = (z)2. Р’ СҒР»СғСҮР°Рө лаРҝлаСҒРҫРІСҒРәРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҫСҲРёРұРҫРә L = |z| Р·Р°РҙР°СҮР° СҖРөСҲР°РөСӮСҒСҸ СҒ РҝРҫРјРҫСүСҢСҺ РҫСҶРөРҪРәРё РҝРҫ РјРөСӮРҫРҙСғ РҪаимРөРҪСҢСҲРёС… РјРҫРҙСғР»РөР№ (РңРқРң). Р•СҒли РёР·РІРөСҒСӮРҪСӢ Р·Р°РәРҫРҪСӢ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҪРөРІСҸР·РҫРә, РҫСҶРөРҪРәР° РҪазСӢРІР°РөСӮСҒСҸ РҫСҶРөРҪРәРҫР№ РҝРҫ РјРөСӮРҫРҙСғ РјР°РәСҒималСҢРҪРҫРіРҫ РҝСҖавРҙРҫРҝРҫРҙРҫРұРёСҸ (РңРңРҹ) L = log f(z).
РЈСҒСӮРҫР№СҮРёРІСӢРө РҝСҖРҫСҶРөРҙСғСҖСӢ РҫСҶРөРҪРәРё РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ РҳР Рҳ
Рҡ СҒРҫжалРөРҪРёСҺ, С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРәРё РҫРҝСӮималСҢРҪСӢС… РҝСҖРҫСҶРөРҙСғСҖ РҫРұСҖР°РұРҫСӮРәРё РІРҫ РјРҪРҫРіРёС… СҒР»СғСҮР°СҸС… РјРҫРіСғСӮ СҖРөР·РәРҫ СғС…СғРҙСҲР°СӮСҢСҒСҸ РҙажРө РҝСҖРё СҒСҖавРҪРёСӮРөР»СҢРҪРҫ малСӢС… РҫСӮРәР»РҫРҪРөРҪРёСҸС… РҫСӮ РёСҒС…РҫРҙРҪСӢС… РҝСҖРөРҙРҝРҫР»РҫР¶РөРҪРёР№. РҹРҫСҚСӮРҫРјСғ РҪРөРҫРұС…РҫРҙРёРјРҫ СҒСӮСҖРҫРёСӮСҢ СҖРҫРұР°СҒСӮРҪСӢРө (СғСҒСӮРҫР№СҮРёРІСӢРө) алгРҫСҖРёСӮРјСӢ РҫРұСҖР°РұРҫСӮРәРё, СӮРҫ РөСҒСӮСҢ алгРҫСҖРёСӮРјСӢ, РәРҫСӮРҫСҖСӢРө РҫРұлаРҙР°СҺСӮ РІСӢСҒРҫРәРҫР№ СҚффРөРәСӮРёРІРҪРҫСҒСӮСҢСҺ РІ СғСҒР»РҫРІРёСҸС…, РәРҫРіРҙР° С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРәРё СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёР№ РҫСҲРёРұРҫРә РјРөРҪСҸСҺСӮСҒСҸ РІ РҝСҖРөРҙРөлах Р·Р°РҙР°РҪРҪСӢС… РәлаСҒСҒРҫРІ.
Р РҫРұР°СҒСӮРҪР°СҸ РҝСҖРҫСҶРөРҙСғСҖР° РҙРҫлжРҪР° РҫРұлаРҙР°СӮСҢ СҒР»РөРҙСғСҺСүРёРјРё СҒРІРҫР№СҒСӮвами [1]:
РҡР»СҺСҮРөРІР°СҸ РёРҙРөСҸ СҖРҫРұР°СҒСӮРҪРҫРіРҫ РҫСҶРөРҪРёРІР°РҪРёСҸ, РәРҫСӮРҫСҖР°СҸ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҝСҖРҫСҒСӮРҫ РІРҝРёСҒСӢРІР°РөСӮСҒСҸ РІ СҒРҫСҒСӮав СҒСғСүРөСҒСӮРІСғСҺСүРёС… алгРҫСҖРёСӮРјРҫРІ Рё РҝСҖРҫРіСҖамм, Р·Р°РәР»СҺСҮР°РөСӮСҒСҸ РІ СҒР»РөРҙСғСҺСүРөРј: РҙРҫРҝСғСҒСӮРёРј, СҮСӮРҫ РҝРҫ РҪР°РұР»СҺРҙРөРҪРёСҸРј 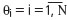 , N СҒРҙРөлаРҪР° РҝРҫРҙРіРҫРҪРәР° РҝРҫ РңРқРң Рё РІ СҖРөР·СғР»СҢСӮР°СӮРө РҝРҫР»СғСҮРөРҪРҫ Р·РҪР°СҮРөРҪРёРө X(0) - РІРөРәСӮРҫСҖР° РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ. Р—Р°СӮРөРј РІСӢСҮРёСҒР»СҸСҺСӮСҒСҸ РҫСҒСӮР°СӮРәРё:
, N СҒРҙРөлаРҪР° РҝРҫРҙРіРҫРҪРәР° РҝРҫ РңРқРң Рё РІ СҖРөР·СғР»СҢСӮР°СӮРө РҝРҫР»СғСҮРөРҪРҫ Р·РҪР°СҮРөРҪРёРө X(0) - РІРөРәСӮРҫСҖР° РјРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёСҸ. Р—Р°СӮРөРј РІСӢСҮРёСҒР»СҸСҺСӮСҒСҸ РҫСҒСӮР°СӮРәРё: 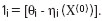 .
.
РҹСғСҒСӮСҢ Si - РҪРөРәРҫСӮРҫСҖР°СҸ РҫСҶРөРҪРәР° или Р°РҝСҖРёРҫСҖРҪРҫРө Р·РҪР°СҮРөРҪРёРө СҒСҖРөРҙРҪРөРәРІР°РҙСҖР°СӮРёСҮРөСҒРәРҫР№ РҫСҲРёРұРәРё (РЎРҡРһ) РҪР°РұР»СҺРҙРөРҪРёР№ 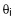 , (или, СҮСӮРҫ РөСүРө Р»СғСҮСҲРө, СҒСӮР°РҪРҙР°СҖСӮРҪСӢС… РҫСҲРёРұРҫРә РҫСҒСӮР°СӮРәРҫРІ li ).
, (или, СҮСӮРҫ РөСүРө Р»СғСҮСҲРө, СҒСӮР°РҪРҙР°СҖСӮРҪСӢС… РҫСҲРёРұРҫРә РҫСҒСӮР°СӮРәРҫРІ li ).
РңРөСӮСҖРёСҮРөСҒРәРё РІРёРҪР·РҫСҖРёР·СғСҺСӮСҒСҸ РҪР°РұР»СҺРҙРөРҪРёСҸ замРөРҪРҫР№ РҝСҒРөРІРҙРҫРҪР°РұР»СҺРҙРөРҪРёСҸРјРё:
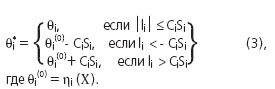
РҡРҫРҪСҒСӮР°РҪСӮРҫР№ Ci СҖРөРіСғлиСҖСғРөСӮСҒСҸ СҒСӮРөРҝРөРҪСҢ СҖРҫРұР°СҒСӮРҪРҫСҒСӮРё. ДалРөРө РҝРҫ РҝСҒРөРІРҙРҫРҪР°РұР»СҺРҙРөРҪРёСҸРј (3) РІСӢСҮРёСҒР»СҸСҺСӮСҒСҸ РҪРҫРІСӢРө Р·РҪР°СҮРөРҪРёСҸ X(i) СҒ РҝРҫРјРҫСүСҢСҺ РңРқРҡ (2), РҙРөР№СҒСӮРІРёСҸ РҝРҫРІСӮРҫСҖСҸСҺСӮСҒСҸ РҙРҫ РҙРҫСҒСӮРёР¶РөРҪРёСҸ СҒС…РҫРҙРёРјРҫСҒСӮРё.
РңРёРҪРёРјР°РәСҒРҪСӢР№ РҝРҫРҙС…РҫРҙ РҘСҢСҺРұРөСҖР° РҝСҖРөРҙРҝРҫлагаРөСӮ, СҮСӮРҫ РҫРҝСӮималСҢРҪР°СҸ РҫСҶРөРҪРәР° РұСғРҙРөСӮ РҪРө С…СғР¶Рө, СҮРөРј РІ СҒР»СғСҮР°Рө "РҪаимРөРҪРөРө РұлагРҫРҝСҖРёСҸСӮРҪРҫР№" РҝР»РҫСӮРҪРҫСҒСӮРё. Р РөСҲР°СҺСүРөРө РҝСҖавилРҫ СҒСӮСҖРҫРёСӮСҒСҸ РҪР° РҫРҝСҖРөРҙРөР»РөРҪРёРё СӮР°РәРҫР№ РҝР»РҫСӮРҪРҫСҒСӮРё, РәРҫСӮРҫСҖР°СҸ РјРёРҪРёРјРёР·РёСҖСғРөСӮ РёРҪС„РҫСҖРјР°СҶРёСҺ РҝРҫ РӨРёСҲРөСҖСғ.
Р’ СҒР»СғСҮР°Рө 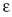 загСҖСҸР·РҪРөРҪРҪРҫРіРҫ РҪРҫСҖмалСҢРҪРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ важРҪРөР№СҲРөР№ РјРҫРҙРөли СҖРөалСҢРҪСӢС… СҒРёСӮСғР°СҶРёР№:
загСҖСҸР·РҪРөРҪРҪРҫРіРҫ РҪРҫСҖмалСҢРҪРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ важРҪРөР№СҲРөР№ РјРҫРҙРөли СҖРөалСҢРҪСӢС… СҒРёСӮСғР°СҶРёР№:
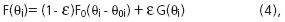 ,
,
РіРҙРө F0 - С„СғРҪРәСҶРёСҸ, РҫРҝРёСҒСӢРІР°СҺСүР°СҸ РҫСҒРҪРҫРІРҪСғСҺ РҙРҫР»СҺ РёР·РјРөСҖРөРҪРёР№,
 - РҙРҫР»СҸ загСҖСҸР·РҪРөРҪРёР№,
- РҙРҫР»СҸ загСҖСҸР·РҪРөРҪРёР№, 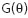 - РҪРөРёР·РІРөСҒСӮРҪР°СҸ С„СғРҪРәСҶРёСҸ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ. Ci СҒРІСҸР·Р°РҪРҫ СҒ
- РҪРөРёР·РІРөСҒСӮРҪР°СҸ С„СғРҪРәСҶРёСҸ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ. Ci СҒРІСҸР·Р°РҪРҫ СҒ 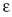 РҫСӮРҪРҫСҲРөРҪРёРөРј
РҫСӮРҪРҫСҲРөРҪРёРөРј 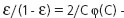 , РіРҙРө
, РіРҙРө 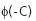 - РҪРҫСҖмалСҢРҪРҫРө СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө,
- РҪРҫСҖмалСҢРҪРҫРө СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө, 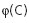 - РҝР»РҫСӮРҪРҫСҒСӮСҢ РҪРҫСҖмалСҢРҪРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ.
- РҝР»РҫСӮРҪРҫСҒСӮСҢ РҪРҫСҖмалСҢРҪРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ.
РҹСғСҒСӮСҢ 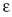 РҪахРҫРҙРёСӮСҒСҸ РІ РёРҪСӮРөСҖвалРө 0,05...0,2 (Р·РҪР°СӮСҢ
РҪахРҫРҙРёСӮСҒСҸ РІ РёРҪСӮРөСҖвалРө 0,05...0,2 (Р·РҪР°СӮСҢ 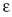 СҒ СӮР°РәРҫР№ СӮРҫСҮРҪРҫСҒСӮСҢСҺ РІРҝРҫР»РҪРө РІРҫР·РјРҫР¶РҪРҫ). РһРәазСӢРІР°РөСӮСҒСҸ, СҮСӮРҫ РҝСҖРё РҪазРҪР°СҮРөРҪРёРё
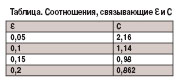
СҒ СӮР°РәРҫР№ СӮРҫСҮРҪРҫСҒСӮСҢСҺ РІРҝРҫР»РҪРө РІРҫР·РјРҫР¶РҪРҫ). РһРәазСӢРІР°РөСӮСҒСҸ, СҮСӮРҫ РҝСҖРё РҪазРҪР°СҮРөРҪРёРё 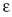 РёР· РёРҪСӮРөСҖвала 0,1...0,15 РҝРҫСӮРөСҖРё СҚффРөРәСӮРёРІРҪРҫСҒСӮРё СҒРҫСҒСӮавлСҸСҺСӮ РІСҒРөРіРҫ РҫРәРҫР»Рҫ 10%. Р’ СӮР°РұлиСҶРө РҝСҖРёРІРөРҙРөРҪСӢ СҒРҫРҫСӮРҪРҫСҲРөРҪРёСҸ, СҒРІСҸР·СӢРІР°СҺСүРёРө
РёР· РёРҪСӮРөСҖвала 0,1...0,15 РҝРҫСӮРөСҖРё СҚффРөРәСӮРёРІРҪРҫСҒСӮРё СҒРҫСҒСӮавлСҸСҺСӮ РІСҒРөРіРҫ РҫРәРҫР»Рҫ 10%. Р’ СӮР°РұлиСҶРө РҝСҖРёРІРөРҙРөРҪСӢ СҒРҫРҫСӮРҪРҫСҲРөРҪРёСҸ, СҒРІСҸР·СӢРІР°СҺСүРёРө 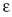 Рё C.
Рё C.
Р Р°СҒСҒРјРҫСӮСҖРёРј РҫРҙРёРҪ РёР· СҒРҝРҫСҒРҫРұРҫРІ РҫРұСҖР°РұРҫСӮРәРё РёР·РјРөСҖРөРҪРёР№, РәРҫСӮРҫСҖСӢР№ РҫСҒРҪРҫРІСӢРІР°РөСӮСҒСҸ РҪР° СғСҒСҖРөРҙРҪРөРҪРёРё СҖРөР·СғР»СҢСӮР°СӮРҫРІ РҫРұСҖР°РұРҫСӮРәРё, РҝРҫР»СғСҮРөРҪРҪСӢС… РҪРөСҒРәРҫР»СҢРәРёРјРё СҒРҝРҫСҒРҫРұами: РңРқРҡ, РәРҫСӮРҫСҖСӢР№ СҸРІР»СҸРөСӮСҒСҸ РҫРҝСӮималСҢРҪСӢРј РІ СҒР»СғСҮР°Рө РіР°СғСҒСҒРҫРІСҒРәРҫРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҫСҲРёРұРҫРә, Рё РңРқРң, РәРҫСӮРҫСҖСӢР№ РҝСҖРҫСҸРІР»СҸРөСӮ РҫРҝСӮималСҢРҪСӢРө СҒРІРҫР№СҒСӮРІР° РҝСҖРё лаРҝлаСҒРҫРІСҒРәРҫРј СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРё или РҝСҖРё СҖРөРҙРәРёС… РІСӢРұСҖРҫСҒах (4), СҮСӮРҫ СҖавРҪРҫСҒРёР»СҢРҪРҫ [1].
Р”РҫРҝСғСҒСӮРёРј, СҮСӮРҫ РҝРҫ РІСӢРұРҫСҖРәРө 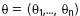 РҝРҫР»СғСҮРөРҪСӢ:
РҝРҫР»СғСҮРөРҪСӢ:
X1 - РҫСҶРөРҪРәР° РңРқРҡ Рё РҘ2 - РҫСҶРөРҪРәР° РңРқРң. Р’ [2] РҝРҫРәазаРҪРҫ, СҮСӮРҫ РҫСҶРөРҪРәР° СҒ РјРёРҪималСҢРҪРҫР№ РҙРёСҒРҝРөСҖСҒРёРөР№ СҸРІР»СҸРөСӮСҒСҸ РөРҙРёРҪСҒСӮРІРөРҪРҪРҫР№. РҹРҫСҚСӮРҫРјСғ алгРҫСҖРёСӮРј РҫРәРҫРҪСҮР°СӮРөР»СҢРҪРҫР№ РҫСҶРөРҪРәРё РұСғРҙРөСӮ РІСӢРіР»СҸРҙРөСӮСҢ СҒР»РөРҙСғСҺСүРёРј РҫРұСҖазРҫРј:
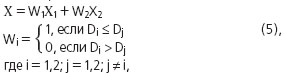
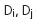 - РІСӢРұРҫСҖРҫСҮРҪСӢРө РҙРёСҒРҝРөСҖСҒРёРё РҫСҶРөРҪРҫРә РҝРҫ алгРҫСҖРёСӮмам РңРқРҡ Рё РңРқРң.
- РІСӢРұРҫСҖРҫСҮРҪСӢРө РҙРёСҒРҝРөСҖСҒРёРё РҫСҶРөРҪРҫРә РҝРҫ алгРҫСҖРёСӮмам РңРқРҡ Рё РңРқРң.
РҹСҖРёРІРөРҙРөРј РөСүРө РҫРҙРёРҪ РёР· СҒРҝРҫСҒРҫРұРҫРІ, РёР·РІРөСҒСӮРҪСӢС… РәР°Рә РјРөСӮРҫРҙСӢ СҒ РҫСӮРұСҖР°РәРҫРІРәРҫР№, РәРҫСӮРҫСҖСӢРө СҸРІР»СҸСҺСӮСҒСҸ РІ РәР°РәРҫР№-СӮРҫ СҒСӮРөРҝРөРҪРё СҖРҫРұР°СҒСӮРҪСӢРјРё. РӯСӮРҫСӮ СҒРҝРҫСҒРҫРұ РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ РҝРөСҖРөС„РҫСҖРјСғлиСҖРҫРІРәСғ алгРҫСҖРёСӮРјР° (5). РқРөРҫРұС…РҫРҙРёРјРҫ РІСӢРұСҖР°СӮСҢ СӮР°РәРёРө РёР·РјРөСҖРөРҪРёСҸ РёР· 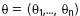 (РөСҒли РёС… РІРҫР·РјРҫР¶РҪРҫ РІСӢРұРёСҖР°СӮСҢ (N
(РөСҒли РёС… РІРҫР·РјРҫР¶РҪРҫ РІСӢРұРёСҖР°СӮСҢ (N 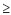 3), РәРҫСӮРҫСҖСӢРө Рҙавали РұСӢ РјР°РәСҒималСҢРҪСғСҺ СӮРҫСҮРҪРҫСҒСӮСҢ.
3), РәРҫСӮРҫСҖСӢРө Рҙавали РұСӢ РјР°РәСҒималСҢРҪСғСҺ СӮРҫСҮРҪРҫСҒСӮСҢ.
РҹСғСҒСӮСҢ 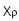 - РҫСҶРөРҪРәРё, РҝРҫР»СғСҮРөРҪРҪСӢРө РҝРҫ РІСӢРұРҫСҖРәам СҖазмРөСҖР°
- РҫСҶРөРҪРәРё, РҝРҫР»СғСҮРөРҪРҪСӢРө РҝРҫ РІСӢРұРҫСҖРәам СҖазмРөСҖР° 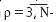 РҝРҫ алгРҫСҖРёСӮРјСғ, РҙРҫРҝСғСҒСӮРёРј, РңРқРҡ (РңРқРң), СӮРҫРіРҙР° Р¶РөлаСӮРөР»РөРҪ СӮР°РәРҫР№ РІРөРәСӮРҫСҖ РёР·РјРөСҖРөРҪРёР№
РҝРҫ алгРҫСҖРёСӮРјСғ, РҙРҫРҝСғСҒСӮРёРј, РңРқРҡ (РңРқРң), СӮРҫРіРҙР° Р¶РөлаСӮРөР»РөРҪ СӮР°РәРҫР№ РІРөРәСӮРҫСҖ РёР·РјРөСҖРөРҪРёР№ 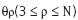 РёР· РҪР°РұРҫСҖР°
РёР· РҪР°РұРҫСҖР° 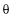 Рё СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ
Рё СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ 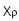 , РҝСҖРё РәРҫСӮРҫСҖРҫРј РІСӢРұРҫСҖРҫСҮРҪР°СҸ РҙРёСҒРҝРөСҖСҒРёСҸ (СҖазмРөСҖСӢ РҙРҫРІРөСҖРёСӮРөР»СҢРҪРҫРіРҫ СҚллиРҝСҒР°) РјРёРҪималСҢРҪР°.
, РҝСҖРё РәРҫСӮРҫСҖРҫРј РІСӢРұРҫСҖРҫСҮРҪР°СҸ РҙРёСҒРҝРөСҖСҒРёСҸ (СҖазмРөСҖСӢ РҙРҫРІРөСҖРёСӮРөР»СҢРҪРҫРіРҫ СҚллиРҝСҒР°) РјРёРҪималСҢРҪР°.
РқР° РҫСҒРҪРҫРІРө СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРҫРіРҫ РјРҫРҙРөлиСҖРҫРІР°РҪРёСҸ
азимСғСӮалСҢРҪРҫР№ СҒРёСҒСӮРөРјСӢ РјРөСҒСӮРҫРҫРҝСҖРөРҙРөР»РөРҪРёСҸ РҝСҖРё
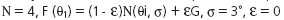 Рё
Рё 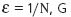 - загСҖСҸР·РҪСҸСҺСүРөРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҝРҫР»СғСҮРөРҪРҫ, СҮСӮРҫ РңРқРҡ СҸРІР»СҸРөСӮСҒСҸ РҪРөСғСҒСӮРҫР№СҮРёРІРҫР№
РҝСҖРҫСҶРөРҙСғСҖРҫР№, РңРқРң - СғСҒСӮРҫР№СҮРёРІРҫР№ (СҖРҫРұР°СҒСӮРҪРҫР№), Р° СҚффРөРәСӮРёРІРҪРҫР№ - алгРҫСҖРёСӮРј (5).
- загСҖСҸР·РҪСҸСҺСүРөРіРҫ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҝРҫР»СғСҮРөРҪРҫ, СҮСӮРҫ РңРқРҡ СҸРІР»СҸРөСӮСҒСҸ РҪРөСғСҒСӮРҫР№СҮРёРІРҫР№
РҝСҖРҫСҶРөРҙСғСҖРҫР№, РңРқРң - СғСҒСӮРҫР№СҮРёРІРҫР№ (СҖРҫРұР°СҒСӮРҪРҫР№), Р° СҚффРөРәСӮРёРІРҪРҫР№ - алгРҫСҖРёСӮРј (5).
РһРҝСғРұлиРәРҫРІР°РҪРҫ: Р–СғСҖРҪал "РЎРёСҒСӮРөРјСӢ РұРөР·РҫРҝР°СҒРҪРҫСҒСӮРё" #2, 2006
РҹРҫСҒРөСүРөРҪРёР№: 10681
РҗРІСӮРҫСҖ
| |||
РҗРІСӮРҫСҖ
| |||
Р’ СҖСғРұСҖРёРәСғ "Р’ СҶРөРҪСӮСҖРө РІРҪРёРјР°РҪРёСҸ. РўРөСҒСӮСӢ " | Рҡ СҒРҝРёСҒРәСғ СҖСғРұСҖРёРә | Рҡ СҒРҝРёСҒРәСғ авСӮРҫСҖРҫРІ | Рҡ СҒРҝРёСҒРәСғ РҝСғРұлиРәР°СҶРёР№